در مطالب قبلی، مفهوم ارزش زمانی پول و نحوهٔ محاسبهٔ ارزش آتی و فعلی توضیح داده شد. در این مطلب یکی از اشکال خاص جریان وجه نقد که مجموعه‌ای از اقساط مساوی است که از زمان یک شروع شده و تا n ادامه می‌یابد، مورد بررسی قرار می‌گیرد.

در بسیاری از موارد با موقعیت‌هایی مواجه می‌شویم که در آن، تمامی جریانات نقدی چندگانه مساوی هستند. مثلاً در نوع رایجی از طرح‌های بازپرداخت وام، از وام‌گیرنده خواسته می‌شود مبلغ وام را در چند قسط مساوی بازپرداخت کند. تقریباً در تمام وام‌های مصرفی (مانند وام‌های اتومبیل و وام‌های دانشجویی) و وام‌های مسکن (که وثیقه هم دارند) اقساط بازپرداخت مساوی است و معمولاً به صورت ماهانه پرداخت می‌شود. به طور کلی، مجموعه جریانات نقدی مساوی که در طول دوره‌هایی با تعداد معین، در انتهای هر دوره رخ می‌دهد، اقساط مساوی عادی نامیده می‌شود. روش‌های ساده‌ای برای ارزیابی این جریانات نقدی وجود دارد که در این مطلب به آن پرداخته می‌شود.
ارزش فعلی اقساط مساوی
در صورتی که از اولین سال در پایان هر سال، سالیانه C تومان دریافت کنیم (طی n سال) ارزش فعلی اقساط مساوی از رابطهٔ زیر بدست می‌آید: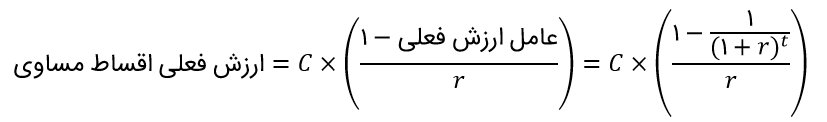

مثال: فرض کنید در حال بررسی یک سرمایه‌گذاری هستید که در پایان هر سه سال آینده ۵۰۰،۰۰۰ تومان به شما می‌پردازد. جریانات نقدی حاصل از این سرمایه‌گذاری به شکل اقساط مساوی سه ساله، ۵۰۰،۰۰۰ تومان است. اگر بخواهید از محل این سرمایه‌گذاری ده درصد بازده کسب کنید، برای این سرمایه‌گذاری چند تومان می‌پردازید؟
با توجه به مباحث قبلی می‌توانیم پس از تنزیل هر یک از جریانات نقدی مذکور به زمان حال با نرخ ده درصد، مجموع ارزش فعلی را محاسبه کنیم:
جهت یادآوری، فرمول ارزش فعلی برابر است با:

استفاده از این روش برای محاسبهٔ ارزش فعلی جریانات نقدی مساوی مناسب است، اما در برخی از مواقع با موقعیت‌هایی مواجه شوید که تعداد جریانات نقدی بسیار زیاد است. مثلاً یک وام مسکن طی ۲۵ سال در اقساط ماهانه بازپرداخت می‌شود. در این مورد ۳۰۰ جریان نقدی وجود دارد که بسیار زیاد است. بهتر است برای محاسبهٔ ارزش فعلی اقساط مساوی چنین وامی از راه‌حل‌های میانبر استفاده شود.
در این معادله، C مبلغ جریان نقدی در هر دوره، r نرخ تنزیل یا نرخ بازده و t تعداد دوره‌هاست. و عبارت ذیل، عامل ارزش فعلی اقساط مساوی نامیده می‌شود:




در این مثال، نرخ بهره ده درصد است و سه جریان نقدی سالانه وجود دارد. پس عامل ارزش فعلی برابر است با: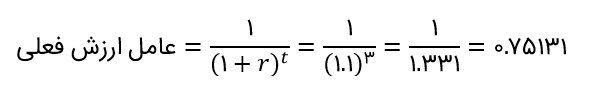



بنابراین عامل ارزش فعلی اقساط مساوی به شکل زیر محاسبه می‌شود:




اکنون می‌توانیم مانند آنچه در محاسبات مربوط به ارزش فعلی یک جریان نقدی انجام دادیم، ارزش فعلی اقساط مساوی۵۰۰،۰۰۰ تومانی را محاسبه کنیم:


مثال: فرض نمایید شما وامی به مبلغ ۱۰۰،۰۰۰ تومان در زمان صفر دریافت می‌نمایید. اقساط مساوی وام در انتهای سال‌های اول تا پنجم پرداخت می‌شود، با فرض نرخ تنزیل ۱۰ درصد مبلغ هر قسط را محاسبه نمایید.
در این سؤال ارزش فعلی وام برابر با ۱۰۰،۰۰۰ تومان ، t=۵، r=۱۰%، است. دقت نمایید که مبلغ وام در واقع برابر است با ارزش فعلی اقساط وام. با جایگذاری در فرمول خواهیم داشت: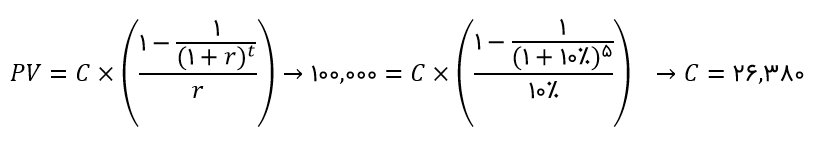

مثال: فرض کنید پس از بررسی دقیق بودجه خود به این نتیجه رسیده‌اید که می‌توانید هر ماه ۶۳۲،۰۰۰ تومان به عنوان قسط یک اتومبیل جدید بپردازید. پس از مراجعه به وب‌سایت بانکی که در آن حساب دارید، مشاهده می‌کنید که نرخ بهره ماهانهٔ فعلی به مدت ۴۸ ماه، یک درصد است. چه مبلغی می‌توانید از این بانک وام بگیرید؟
برای پاسخ به این سؤال باید ارزش ۴۸ قسط مساوی ۶۳۲،۰۰۰ تومان را با نرخ بهره یک درصد محاسبه کنیم. اقساط وام همگی مساوی است، بنابراین عامل ارزش فعلی اقساط این وام برابر است با: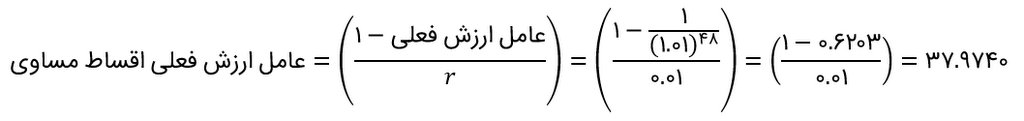

با استفاده از این عامل می‌توانیم ارزش فعلی ۴۸ قسط مساوی ۶۳۲،۰۰۰ تومان را به صورت زیر محاسبه کنیم:

پس می‌توانید با نرخ ماهانه یک درصد، ۲۳،۹۹۹،۵۶۸ تومان وام بگیرید و آن را با اقساط ۶۳۲،۰۰۰ تومانی بازپرداخت کنید.
مثال: فرض کنید برای تأمین هزینهٔ مسافرت در تعطیلات، پول کافی در اختیار ندارید؛ بنابراین با استفاده از کارت اعتباری خود ۱،۰۰۰،۰۰۰ تومان وام می‌گیرد و باید هر ماه ۲۰،۰۰۰ تومان از وام خود را بپردازید. نرخ بهره ماهانهٔ این اعتبار ۱/۵ درصد است. چند ماه طول می‌کشد تا وام مذکور را تسویه کنید؟
در این سؤال، مبلغ هر قسط ۲۰،۰۰۰ تومان و نرخ بهره ماهانه ۱/۵ درصد است؛ اما مدت زمان بازپرداخت (تعداد ماه‌‌ها) مشخص نیست، ارزش فعلی وام هم ۱،۰۰۰،۰۰۰ تومان است. با استفاده از روابط جبری، می‌توانیم این سؤال را حل کنیم: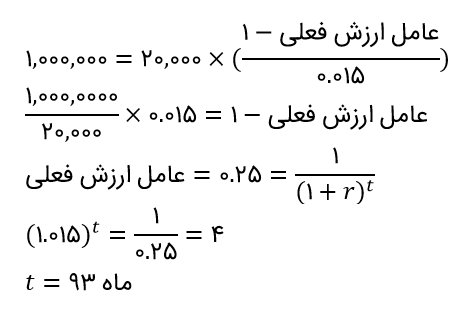

بنابراین تقریباً ۷/۷۵ سال (۹۳ تقسیم بر ۱۲ ماه) طول می‌کشد تا ۱،۰۰۰،۰۰۰ تومان مذکور را با نرخ ماهانه ۱/۵ درصد بازپرداخت کنید.