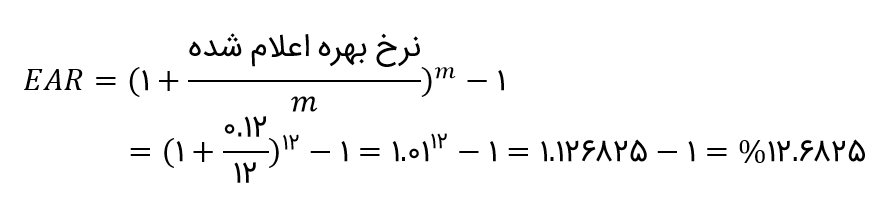در مطالب قبلی نحوهٔ محاسبهٔ ارزش فعلی و آتی پول با کمک نرخ بهرهٔ ساده و مرکب توضیح داده شد. در مثالهای ذکر شده در این مطالب، نرخ بهره به صورت نرخ سالیانه معرفی شد. زمانی که دورهٔ مرکب شدن کمتر و یا بیشتر از یک سال باشد بحث نرخهای اسمی و مؤثر پیش میآید. برای دورههای کمتر و یا بیشتر از یک سال، باید در نحوهٔ محاسبات، تغییراتی لحاظ شود.
نرخ بهرهٔ اسمی
برای مثال در نظر بگیرید، نرخ بهره به صورت ماهیانه ۲% محاسبه شود. در این صورت بهرهٔ سالیانه برابر با ۲۴٪=۲٪x۱۲ است که به آن نرخ اسمی سالیانه گفته میشود. نکتهای که وجود دارد این است که در این مثال برای محاسبهٔ بهرهٔ سالیانه، ارزش زمانی پول در نظر گرفته نشده است. در صورت لحاظ کردن ارزش زمانی پول، نرخ بهرهٔ سالیانه بیشتر خواهد شد. این نرخ «نرخ مؤثر سالیانه» نامیده میشود.
نرخ بهره مؤثر سالانه
اگر نرخ بهرهٔ سالانه، ده درصد باشد و هر شش ماه مرکب شود، یعنی درواقع از محل این سرمایهگذاری هر شش ماه ۵ درصد بهره دریافت میکنید. سؤالی که در این زمینه مطرح میشود این است که آیا پنج درصد ششماهه با نرخ ۱۰ درصد سالانه برابر است؟ به راحتی میتوان گفت خیر. اگر شما یک میلیون تومان را با نرخ ۱۰ درصد سالانه سرمایهگذاری کنید، در پایان سال یک میلیون و صد هزار تومان خواهید داشت. ولی اگر همین یک میلیون را با نرخ پنج درصد ششماهه سرمایهگذاری کنید، ارزش آتی این سرمایهگذاری برابر است با ارزش آتی یک میلیون با نرخ ۵ درصد به مدت دو دوره، به عبارت دیگر، ارزش آتی سرمایهگذاری شما برابر است با:
![]()
در این حالت، ارزش آتی سرمایهگذاری نسبت به حالتی که نرخ سالانه ۱۰ درصد است (و طی سال مرکب نشود)، ۲۵۰۰ تومان بیشتر است. دلیل این امر هم بسیار ساده است، حساب شما پس از شش ماه، پنجاه هزار تومان بستانکار میشود:
![]()
در شش ماه بعدی، پنج درصد این پنجاه هزار تومان را نیز به عنوان بهره دریافت میکنید:
![]()
همانطور که در این مثال میبینید، ۱۰ درصد سالانهای که هر شش ماه مرکب میشود، در واقع برابر است با ۱۰/۲۵ درصد سالانه. به عبارت دیگر، بین ده درصدی که هر شش ماه مرکب میشود و ۱۰/۲۵ درصدی که سالانه مرکب میشود بیتفاوت خواهید بود. هرگاه در طی سال، مرکب کردن بهره وجود داشته باشد، باید در مورد نرخ واقعی بیشتر تأمل کنید.
در این مثال، نرخ بهره ۱۰ درصد اعلام شده است. نرخ ۱۰/۲۵ درصد، یعنی نرخ واقعی که به دست میآورید، نرخ مؤثر سالانه نامیده میشود. هنگام مقایسهٔ سرمایهگذاریها با نرخهای بهره متفاوت، همیشه باید نرخها را به نرخ مؤثر تبدیل کنید. در ادامه، رویههایی که برای انجام مقایسه، مورد استفاده قرار میگیرد، توضیح داده میشود.
محاسبه و مقایسهٔ نرخهای مؤثر سالانه
برای اینکه ببینید چرا باید در بین انواع نرخها، فقط به نرخ مؤثر توجه داشت، فرض کنید، فردی به دنبال بهترین فرصتهای سرمایهگذاری موجود است و با سه پیشنهاد زیر مواجه است:
بانک الف: نرخ بهرهٔ ۱۵ درصد که روزانه مرکب میشود.
بانک ب: نرخ بهرهٔ ۱۵/۵ درصد که سه ماهه مرکب میشود.
بانک ج: نرخ بهرهٔ ۱۶ درصد که سالانه مرکب میشود.
اگر این فرد ۱،۰۰۰،۰۰۰ تمومان سرمایه داشته باشد، کدام یک از فرصتهای فوق، برای افتتاح یک حساب پسانداز بهتر است؟ اگر فرد بخواهد همین مبلغ را وام بگیرید، کدام بانک بهترین پیشنهاد را میدهد؟
ابتدا شرایط بانک ج را بررسی میکنیم. این بانک نرخ ۱۶ درصد سالانه را پیشنهاد میدهد. از آنجا که این بانک طی سال بهره را مرکب نمیکند، نرخ مؤثر آن ۱۶ درصد است. نرخ پیشنهادی بانک ب ۱۵/۵ درصد سالانه، یا ۳/۸۷۵ درصد سه ماهه است. با این نرخ، ارزش آتی یک میلیون تومان برای چهار دوره، برابر است با:
![]()
بنابراین نرخ بهره مؤثر سالانه این بانک ۱۶/۴۲ درصد است. از نظر فردی که قصد دارد حساب پسانداز افتتاح کند، این نرخ نسبت به نرخ پیشنهادی بانک ج خیلی مناسب تر است، ولی در عوض از نظر وام گیرنده، نرخ بانک ج نامناسبتر است.
در بانک الف، موجودی شما به صورت روزانه مرکب میشود. ممکن است این حالت کمی غیرعادی به نظر برسد، ولی محاسبه بهره روزانه هم بسیار رایج است. در این حالت نرخ بهره روزانه برابر است با:
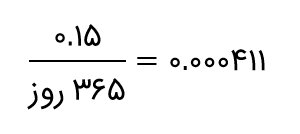
بنابراین، نرخ بهره روزانه ۰/۰۴۱۱ درصد است. با این نرخ، ارزش آتی یک سرمایهگذاری یک میلیون تومانی برای دورههای 365 روزه برابر است با:
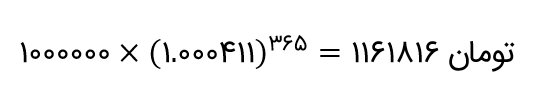
پس نرخ مؤثر سالانه بانک الف ۱۶/۱۸ درصد است. از نظر یک سرمایهگذار این نرخ در مقایسه با نرخ مؤثر سالانه بانک ب (۱۶/۴۲ درصد) جذابیت کمتری دارد ولی از نظر وام گیرنده به خوبی نرخ مؤثر سالانه بانک ج، یعنی ۱۶ درصد نیست.
این مثال دو نکته را خاطر نشان میسازد:
۱. بالاترین نرخ اعلام شده لزوماً بهترین نرخ نیست.
۲. مرکب کردن طی دوره میتواند موجب اختلاف بسیار زیاد بین نرخ بهره اعلام شده و نرخ مؤثر شود. به خاطر داشته باشید نرخ مؤثر، نرخ واقعی است که دریافت یا پرداخت میکنید.
اگر به این مثال دقت کنید، میبینید که نرخ مؤثر سالانه طی سه مرحله محاسبه میشود. ابتدا نرخ اعلام شده را به دفعاتی که بهره مرکب میشود، تقسیم میکنیم. سپس عدد یک را به نتیجه مرحله اول اضافه میکنیم. در ادامه، عدد یک را به نتیجهٔ مرحله اول اضافه میکنیم و حاصل جمع را به توان تعداد دفعاتی که بهره مرکب میشود، میرسانیم. در نهایت، عدد یک را از نتیجه مرحله دوم کسر میکنیم. به طور کلی، اگر تعداد دفعاتی که بهره طی سال مرکب میشود، برابر m باشد، نرخ بهرهٔ مؤثر سالانه ( (EAR با استفاده از رابطهٔ زیر محاسبه میشود:

با استفاده از فرمول بالا می توانیم تأثیر تناوب پرداخت سود را مشاهده نماییم. مثلاً فرض کنید که یک سرمایهگذاری با نرخ سالانه ۱۲ درصد به شما پیشنهاد شده است و بهره را ماهانه مرکب میکند. در این حالت، طی سال، بهره ۱۲ بار مرکب میشود، بنابراین m برابر است با ۱۲. اکنون میتوانید نرخ مؤثر سالانه این سرمایهگذاری را محاسبه کنید: