یکی از مسائل اساسی که مدیران مالی با آن روبه‌رو هستند، تعیین ارزش فعلی جریانات نقدی مورد انتظار آینده است. به بیان دیگر می‌توان گفت پول دارای دو بعد است، یک بعد، مبلغ پرداختی و بعد دیگر زمان پرداخت. لذا هنگامی که در مورد رد و بدل شدن پول صحبت می‌شود علاوه بر مبلغ آن باید به زمان پرداخت نیز اشاره شود. از همین رو است که در مباحث مالی برای صحبت در مورد جابجایی پول معمولاً از نمودار زمانی مشابه نمودار ذیل استفاده می‌شود.

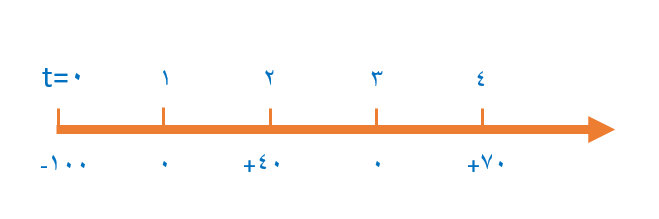
نمودار زمانی پول، نشان‌دهندهٔ میزان جابجایی پول از دید یک شخص (مثلاً سرمایه‌گذار) است. در این نمودار عدد صفر نشان دهندهٔ ابتدای دورهٔ اول (معمولاً زمان حال و یا زمان شروع یک پروژه به عنوان زمان صفر در نظر گرفته می‌شود). عدد یک نشان دهندهٔ انتهای دورهٔ اول و ابتدای دورهٔ دوم است به همین ترتیب عدد ۲ و ۳ ... تا n. مطابق نمودار، سرمایه‌گذار در سال صفر مبلغ 100 تومان پرداخت نموده است (علامت منفی به معنای پرداخت وجه و علامت مثبت به معنای دریافت وجه است). این سرمایه‌گذار در زمان‌های ۲ و ۴ به ترتیب مبالغ ۴۰ و ۷۰ تومان را دریافت نموده است.
بسیاری از افراد، دلیل در نظر گرفتن ارزش زمانی پول را مسئلهٔ تورم می‌دانند و بیان می‌کنند به دلیل گران شدن اجناس در طی زمان، مبلغی از پول در زمان حال، ارزش بیشتری از همین مبلغ در زمان آینده دارد. به طور کلی یک میلیون تومان امروز بیشتر از یک میلیون تومانی که در آینده دریافت خواهید کرد ارزش دارد. یکی از دلایل این امر در دنیای واقعی آن است که با سرمایه‌گذاری و کسب بازدهی، یک میلیون تومان فعلی شما قابلیت رشد خواهد داشت و ارزش بیشتری پیدا خواهد کرد، بنابراین افراد، یک میلیون تومان حاضر را به یک میلیون تومان سال دیگر ترجیح می‌دهند.
سرمایه گذاری یک دوره‌ای
فرض کنید قصد دارید یک میلیون تومان در حساب پس‌اندازی که سالانه ۱۰ درصد بهره می‌پردازد، سرمایه‌گذاری کنید. پس از یک سال پول شما چقدر خواهد بود؟
اگر مدت سرمایه‌گذای یک دوره و نرخ بهرهٔ آن ۱۰ درصد باشد، سرمایهٔ اولیه مطابق فرمول زیر افزایش می‌یابد. در این حالت سرمایه‌گذار در انتهای سال اول ۱،۱۰۰،۰۰۰ تومان خواهد داشت.

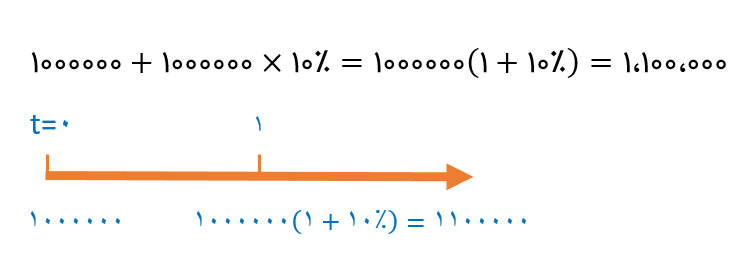
سرمایه‌گذاری چند دوره‌ای
با در نظر گرفتن مثال حالت قبل، اگر نرخ بهره تغییر نکند، پس از دوسال، پول شما چقدر خواهد بود؟
اگر سال دوم فقط اصل پول، در حساب پس انداز مذکور سرمایه‌گذاری شود و از سرمایه‌گذای مجدد بهرهٔ سال اول صرف نظر شود، در سال دوم مبلغ ۱،۰۰۰،۰۰۰ تومان در نرخ بهرهٔ ۱۰٪ ضرب خواهد شد و در نتیجه، ۱۰۰،۰۰۰ تومان به پول اضافه خواهد شد.

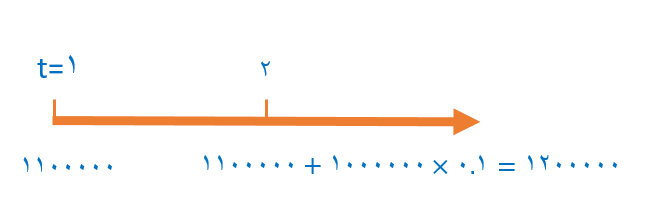
در مثال قبل محاسبات با فرض نرخ بهرهٔ ساده صورت گرفته است. بهرهٔ ساده، بهره‌ای است که فقط به اصل پول تعلق می‌گیرد در حالی که بهرهٔ مرکب بهره‌ای است که به کل پول (اعم از اصل و فرع) تعلق می‌گیرد. در مطالب بعدی محاسبهٔ ارزش زمانی پول با استفاده از بهرهٔ مرکب به تفصیل توضیح داده خواهد شد.